The Mechanical Speed Control for the Conical Pendulum

There is a basic difference between the classic pendulum and the conical pendulum:

In the classic pendulum and for small swings the period of swing is approximately the same for different size swings: that is, the period is independent of amplitude. This property, called isochronism, is the reason pendulums are so useful for timekeeping. Successive swings of the pendulum, even if changing in amplitude, take the same amount of time. The basic formula for the ideal pendulum is:

So for small swing angles (much less than 1 radian (57 degrees) the period of the oscillation will depend basically of the length on the pendulum.

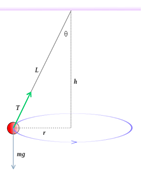
In the conical pendulum: the period of rotation for small angles θ is determined by the length of the pendulum.

The formulas for the conical pendulum are:

Where t is the period of revolution

This formula can be expressed as:

When applying a force to keep the pendulum rotating, there will be a centrifugal force that will increase the angle θ so h will be smaller as the angle increases and the period of revolution will be smaller. In theory for small forces there will be equilibrium and the angle and the speed will be constant (for small angles).

In real life and with imperfect arbors and wood susceptible for changes by temperature and humidity the equilibrium point will constantly change. Sometimes, when the friction is low the pendulum will rotate faster  (larger angle) and when there is more friction the speed will be slower (smaller angle) because we are applying a constant rotation torque with the impulse motor.

The above means that the conical pendulum is intrinsically inaccurate for time keeping unless we add some kind of regulation and this has been the challenge for all conical pendulum clock designs since they were invented. The patent of J. C. Briggs in 1885 is related to a speed control device that increases the friction as the angle of the pendulum grows. But in reality this is basically what the Watt’s speed governor does.

My challenge was to find a way to make a very simple speed control for my conical clock and I did it!

I added a small piece of wood cut in a parabolic shape. The pendulum rod’s tip will hit the piece of wood when the angle increases due to speed and this will force a reduction of the angle and will slow down the rotation speed.

In the flowing slow motion video (1/8^th of the real speed where on revolution is 8 seconds) you can see how this device works and slows down the pendulum speed.